I ragazzi della 3AS, durante l’ora di scienze, hanno usato delle monetine per modellizzare il decadimento radioattivo, ma come è possibile? Per avere la risposta non dovrete fare altro che leggere il resto dell’articolo.

Materiali: 1 contenitore con coperchio

                100 centesimi (100 monetine da 1 centesimo)

                carta millimetrata

                penna o matita

Ma che cosa è il decadimento radioattivo? 

Il decadimento radioattivo è un processo in cui gli isotopi emettono spontaneamente particelle. 

Le monetine sono ottimi modelli per gli isotopi perché lanciando una moneta si ha ½ probabilità che esca testa e ½  di probabilità che esca croce. Ogni lancio è un evento indipendente perché il risultato di un lancio non è influenzato dai lanci precedenti. 

Come prima cosa abbiamo messo tutte le monete nella scatola chiusa dal coperchio,  abbiamo agitato la scatola per diversi secondi  per poi rimuovere il coperchio e versare le monete su una superficie piana. 

Abbiamo poi rimosso tutte le monete con la testa rivolta verso l’ alto, sottratto la loro quantità dal totale, inserito il numero di monete restanti nella tabella (riga del lancio 1 e trial) e messo le monete rimosse in linea. Una volta raccolti i centesimi rimanenti li abbiamo rilanciati, tolto quelli con testa, annotato il numero delle restanti e messo le monete tolte in una linea accanto a quella fatta precedentemente. 

Questo procedimento è durato fino all’esaurimento delle monete, una volta finite, abbiamo rifatto lo stesso procedimento per un totale di 4 trial. 

Finiti i trial, abbiamo trovato il valore medio di ogni riga contenente i lanci e inserito all’interno di un diagramma cartesiano le monete (asse delle ordinate) e i lanci (asse ascisse) trovando la curva di decadimento 

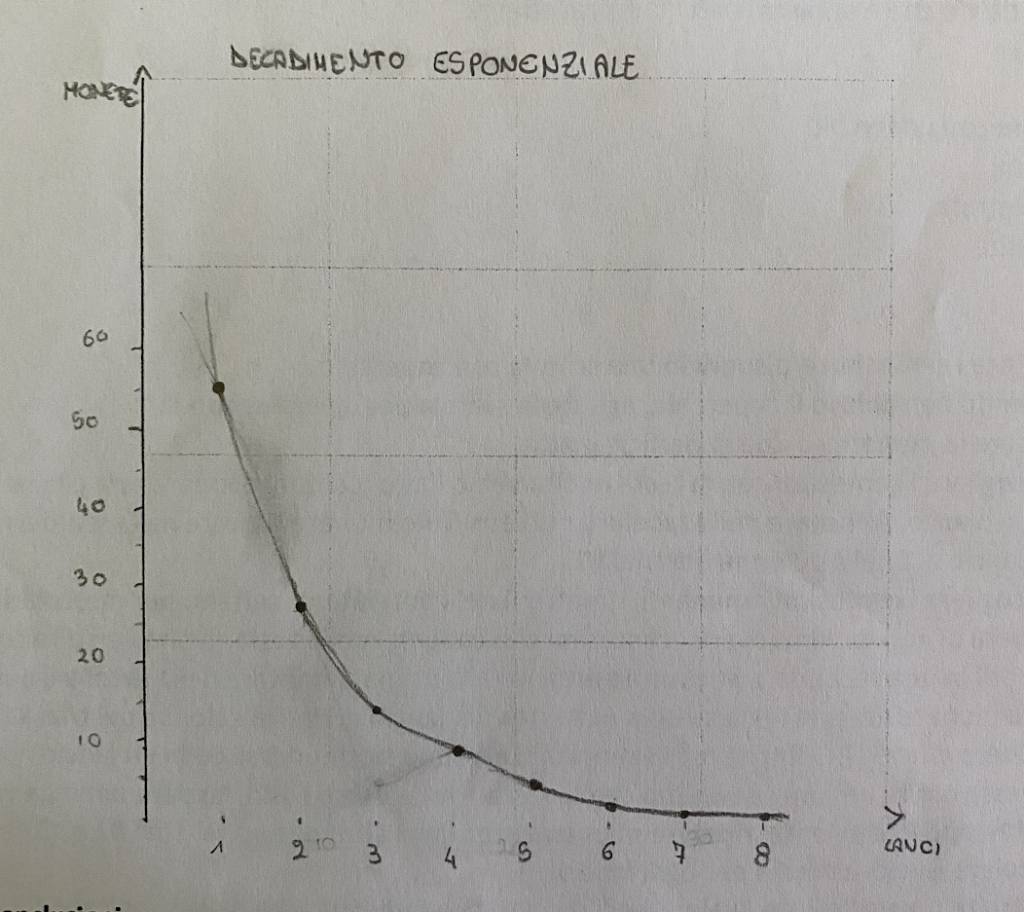
Cosa è successo? 

La probabilità che per ogni centesimo esca testa ad ogni lancio è del 50%. Dopo il primo lancio, rimangono circa la metà dei centesimi originali, dopo il secondo ¼  , poi ⅛  e così via.

Questo tipo di pattern, in cui la quantità diminuisce ripetutamente di una frazione fissa, è noto come decadimento esponenziale. 

Ogni volta che si lanciano i centesimi rimanenti, circa la metà viene rimossa. Il tempo necessario per rimuovere la metà dei centesimi rimanenti è detto tempo di dimezzamento o  emivita che in questo caso è circa un lancio.

                                                                                                             Cabrini Annalisa